命令式学习：面向机器人自主性的自监督神经符号学习框架

摘要

尽管强化学习与模仿学习等数据驱动方法在机器人自主性领域取得了显著成就，但其数据依赖的本质仍制约着它们在动态变化环境中的泛化能力。此外，针对机器人任务的大规模数据采集往往面临成本高昂与实施困难的双重挑战。为突破这些限制，我们提出了一种新型自监督神经符号（NeSy）计算框架——命令式学习（IL），通过融合符号推理的泛化优势来提升机器人自主性。

IL框架由三大核心组件构成：

神经模块：负责从原始传感器数据中提取高层次语义特征
推理引擎：基于物理定律、逻辑推理和几何分析等符号化规则进行决策
记忆系统：存储机器人经验与知识表征

我们将IL建模为一种特殊的双层优化（BLO）问题，实现了三个模块间的协同学习机制。这种设计既规避了数据驱动方法对标注数据的高度依赖，又充分结合了符号推理在逻辑一致性、物理规律遵从性和几何可行性等方面的优势。

通过探讨闭式解、一阶优化、约束优化、二阶优化和离散优化等多种技术手段，我们在五类机器人自主性任务中验证了IL的有效性：

路径规划（全局与局部）
规则归纳（逻辑推理）
最优控制（无人机姿态控制）
视觉惯性里程计（SLAM）
多旅行商问题（MTSP）

实验结果表明，IL框架显著提升了机器人系统的自主能力。我们预期该范式将为跨领域研究提供新思路，并推动神经符号学习在复杂机器人场景中的深化应用。

关键词: 神经符号人工智能，自监督学习，双层优化，命令式学习，机器人自主性

1 引言

随着深度学习的快速发展(LeCun et al. 2015)，强化学习(Zhu and Zhang 2021)和模仿学习(Hussein et al.2017)等数据驱动方法在机器人自主性领域引起了广泛关注。然而，尽管取得了显著进展，许多数据驱动的自主系统仍然主要受限于其训练环境，表现出有限的泛化能力(Banino et al. 2018; Albrecht et al. 2022)。

相比之下，人类能够将经验内化为抽象概念或符号知识(Borghi et al. 2017)。例如，无论是城市中的铺砌街道还是森林中的泥土小径，我们都将"道路"和"路径"视为可通行区域的符号或概念(Hockley 2011)。基于这些概念，人类可以运用空间推理在新颖复杂的环境中导航(Strader et al. 2024)。这种对新场景的适应能力源于人类的抽象化和符号化能力，而这一人类智能的基本特征在当前的数据驱动自主机器人中仍然明显缺失(Garcez et al. 2022; Kautz 2022)。

尽管大语言模型（LLMs）的隐式推理能力在近年来备受关注(Lu et al. 2023; Shah et al. 2023a)，但机器人自主系统在实现可解释推理方面仍面临重大挑战。这在几何推理、物理推理和逻辑推理等关键领域尤为明显(Liu et al. 2023)。突破这些限制并将可解释的符号推理融入数据驱动模型——这一方向被称为神经符号（NeSy）推理——将显著提升机器人自主性(Garcez et al. 2022)。

尽管神经符号(NeSy)推理展现出巨大潜力，但其在机器人领域的具体应用仍处于萌芽阶段。这一现状的重要根源在于神经符号推理领域本身仍处于发展阶段，尚未形成严格的定义共识(Kautz 2022)。狭义定义认为，神经符号推理是神经方法（数据驱动）与符号方法的结合体，后者运用形式逻辑和符号进行知识表示及基于规则的推理。广义定义则扩展了"符号"的范畴，认为符号不仅包含逻辑术语，还应涵盖人类可理解的所有概念。这包括物理属性和语义特征，具体体现为：基于具体方程式的建模(Duruisseaux et al. 2023)、逻辑编程(Delfosse et al. 2023)和可编程目标(Yonetani et al. 2021a)等方法。这种广义定义能够涵盖物理规律、逻辑推理、几何分析等多元推理形式。在此语境下，现有文献已涌现诸多神经符号系统实例，例如基于模型的强化学习(Moerland et al. 2023)、物理信息网络(Karniadakis et al. 2021)，以及控制(O’Connell et al. 2022)、任务调度(Gondhi and Gupta 2017)和几何分析(Heidari and Iosifidis 2024)等学习增强型任务。

本文探索了神经符号(NeSy)推理在机器人自主性中的广义定义，提出了一种自监督神经符号学习框架——命令式学习(IL)。该框架旨在解决现有机器人学习范式的四个核心问题：

泛化能力局限
现有数据驱动系统（包括强化学习模型）往往局限于训练环境，难以适应新场景。这种局限性源于其无法习得显性常识规则，制约了知识迁移能力。这促使我们深入研究符号推理技术。
黑箱特性
数据驱动模型的内部因果机制不透明，而机器人任务中的错误决策可能引发严重后果。这种不可解释性促使我们转向更透明的神经符号系统。
标注依赖性强
机器人任务（如模仿学习）的标注成本显著高于计算机视觉任务，因其依赖专业设备而非人工标注。例如机器人运动规划的真值标注涉及复杂动力学特性，凸显自监督学习方法的必要性。
次优整合
神经模块与符号模块的分离训练会导致误差累积，产生次优解。这推动我们研究端到端的神经符号学习方法。

IL通过将符号推理的泛化能力与神经网络的表征学习相结合，构建包含神经模块、推理引擎和记忆系统的三元架构。该框架采用特殊的双层优化范式，使符号系统能指导神经网络学习符号化概念，同时神经网络的反馈优化符号推理过程，形成自我完善的协同机制。

IL框架的提出旨在通过统一设计解决上述问题。其核心灵感来源于一个关键发现：数据驱动模型通常依赖标注数据进行参数优化，而符号推理模型往往无需标签即可运行。然而有趣的是，这两类模型均可采用类梯度下降的迭代优化方法。以几何模型中的集束调整(BA)、物理模型中的模型预测控制(MPC)，以及离散模型中的图结构A*搜索为例，这些符号推理方法虽可视为优化问题，却能在无监督条件下完成优化。IL的创新之处在于建立两类方法的互校正机制，通过强制神经模型与符号模型相互纠偏，形成新型自监督学习范式。

为实现整体框架的优化，IL被建模为特殊的双层优化(BLO)问题。该机制通过将自监督符号模型的误差反向传播至神经模型，实现双向参数更新。"命令式"这一术语的采用，正是为了强调这种由符号推理驱动的被动式自监督学习特性。

本文的核心贡献可总结如下：

• 自监督神经符号学习框架的创新提出
我们探索了面向机器人自主性的自监督神经符号学习框架——命令式学习(IL)。通过将IL建模为特殊的双层优化(BLO)问题，该框架强制神经网络学习符号概念，并利用数据驱动方法增强符号推理能力。这种设计形成了双向协同学习范式，避免了传统解耦系统因误差累积导致的次优解。

• 多元化优化策略的系统整合
针对IL框架的技术挑战，我们提出了系列优化解决方案。具体展示了如何将闭式解、一阶优化、二阶优化、约束优化和离散优化等不同技术有机整合到IL框架中，形成完整的优化体系。

• 开源社区共享与实践验证
为促进技术普惠，我们在路径规划、规则归纳、最优控制、视觉里程计和多机器人路径规划等典型机器人自主任务中系统验证了IL的有效性。相关源代码已在 https://sairlab.org/iseries/ 开源，以期推动更广泛的机器人学研究。

本文研究建立在团队先前在机器人自主性多个领域的工作基础之上，包括局部规划(Yang等,2023)、全局规划(Chen等,2024)、同步定位与建图(SLAM)(Fu等,2024)、特征匹配(Zhan等,2024)以及多智能体路径规划(Guo等,2024)。这些早期研究在不同领域初步实现了命令式学习(IL)的原型框架，但尚未建立机器人自主性领域神经符号(NeSy)学习的系统化方法论。本文通过以下创新填补了这一研究空白：正式定义IL框架体系；深入探讨IL在不同机器人自主任务中的优化挑战；拓展规则归纳和最优控制等新型应用场景。此外，我们基于双层优化(BLO)构建了IL的理论基础，通过五个典型机器人自主任务的实验验证提出多种实用解决方案，并在各领域实验中证明了IL相较现有最优(SOTA)方法的显著优势。

2 相关工作

2.1 双层优化（Bilevel Optimization）

双层优化(BLO)由Bracken和McGill (1973)首次提出并经过数十年发展。经典方法通过将下层问题的最优性条件作为约束，将双层规划问题转化为单层约束优化问题(Hansen et al. 1992; Gould et al. 2016; Shi et al. 2005; Sinha et al. 2017)。近年来，基于梯度的BLO方法因其在现代机器学习和深度学习问题中的高效性而备受关注。由于本文聚焦于学习层面的研究，后续将重点探讨基于梯度的BLO方法，并简要分析其在机器人学习应用中的局限性。

从方法论角度，基于梯度的双层优化(BLO)方法主要可分为近似隐式微分(AID)、迭代微分(ITD)和基于价值函数的三大类方法。基于隐式微分推导上层目标函数梯度(或称超梯度)的显式表达，AID类方法通过广义迭代求解器处理下层问题，同时采用高效的Hessian逆向量积估计技术(Domke 2012; Pedregosa 2016; Liao et al. 2018; Arbel and Mairal 2022a)。ITD类方法则通过前向或反向自动微分模式，沿着灵活的内部优化轨迹直接进行反向传播来近似超梯度(Maclaurin et al. 2015; Franceschi et al. 2017; Finn et al. 2017; Shaban et al. 2019; Grazzi et al. 2020)。基于价值函数的方法将下层问题重构为价值函数约束，并采用混合梯度聚合、对数障碍正则化、原始对偶方法和动态屏障等约束优化技术进行求解(Sabach and Shtern 2017; Liu et al. 2020a; Li et al. 2020a; Sow et al. 2022; Liu et al. 2021b; Ye et al. 2022)。

近年来，大规模随机BLO在理论与实践层面均获得深入研究。例如，Chen et al. (2021)和Ji et al. (2021)提出了基于Neumann级数的超梯度估计器；Yang et al. (2021)、Huang and Huang (2021)、Guo and Yang (2021)、Yang et al. (2021)以及Dagréou et al. (2022)引入了方差缩减与递归动量策略；Sow et al. (2021)则开发了无需计算Hessian或Jacobian矩阵的进化策略(ES)方法。

在理论层面，已有大量研究基于下层问题强凸的关键假设对BLO的收敛性进行了深入分析（Franceschi等人，2018；Shaban等人，2019；Liu等人，2021b；Ghadimi与Wang，2018；Ji等人，2021；Hong等人，2020；Arbel与Mairal，2022a；Dagréou等人，2022；Ji等人，2022a；Huang等人，2022）。其中，Ji与Liang（2021）进一步为确定性BLO在（强）凸上层函数场景下建立了复杂度下界。Guo与Yang（2021）、Chen等人（2021）、Yang等人（2021）以及Khanduri等人（2021）通过引入二阶导数实现了近乎最优的样本复杂度。Kwon等人（2023）和Yang等人（2024）则重点分析了一阶随机BLO算法的收敛性。近期研究开始关注更具挑战性的场景：当下层问题为凸问题或满足Polyak-Lojasiewicz（PL）条件、Morse-Bott条件时（Liu等人，2020a；Li等人，2020a；Sow等人，2022；Liu等人，2021b；Ye等人，2022；Arbel与Mairal，2022b；Chen等人，2023；Liu等人，2021c），相关收敛性分析也取得了突破。更多关于BLO及其理论分析的进展可参考综述文献（Liu等人，2021a；Chen等人，2022）。

BLO技术已成功融入机器学习应用，例如将可微分优化层(Amos and Kolter 2017)、凸优化层(Agrawal et al. 2019)和声明式层(Gould et al. 2021)整合至深度神经网络架构。这些方法已被应用于光流估计(Jiang et al. 2020)、轴心操控(Shirai et al. 2022)、机器人控制(Landry 2021)和轨迹生成(Han et al. 2024)等具体场景。然而，面向机器人自主性的神经符号(NeSy)学习仍缺乏系统性方法论研究。此外，机器人问题往往具有高度非凸性特征，易产生多个局部极小值与鞍点(Jadbabaie et al. 2019)，显著增加优化难度。本文将从理论收敛保障与多任务实证验证两个维度，深入探索适用于机器人自主性任务的BLO优化方法。

2.2 机器人学习框架

我们总结了机器人领域的主要学习框架，包括模仿学习、强化学习和元学习。其他方法将简要提及。

模仿学习

模仿学习是一种通过观察和模仿专家行为使机器人掌握任务的技术。无需显式建模复杂行为，机器人即可完成多种任务，包括灵巧操作（McAleer 等，2018）、导航（Triest 等，2023）和环境交互（Chi 等，2023）等。当前研究聚焦于历史数据利用（Kaufmann 等，2020；Chen 等，2020a；Lee 等，2020）、多模态行为建模、特权教师机制应用，以及通过生成对抗网络（Ho 与 Ermon，2016）、变分自编码器（Zhao 等，2023）和扩散模型（Chi 等，2023）等生成模型进行数据合成。这些进展彰显了模仿学习领域持续活跃的研究态势。

与传统监督学习不同，模仿学习不要求训练数据满足独立同分布（iid）假设，且完全依赖表征"优质"行为的专家数据。这种特性使得测试阶段的微小误差可能引发级联故障。尽管存在通过引入可控误差进行数据增强（Pomerleau，1988；Tagliabue 等，2022；Codevilla 等，2018）和专家咨询实现数据聚合（Ross 等，2011）等技术手段，该领域仍面临显著挑战：数据效率低下问题表现为有限或次优示教严重影响性能；泛化能力不足则源于高质量数据采集的高成本特性，导致机器人难以将习得行为适配到新场景或未遇见的场景变体中。

强化学习与挑战

强化学习（RL）是一种通过与环境交互并以奖励或惩罚形式获得反馈来完成任务的机器学习范式（Li 2017）。凭借其适应性和有效性，RL已被广泛应用于导航（Zhu and Zhang 2021）、机械臂操作（Gu et al. 2016）、移动控制（Margolis et al. 2024）和人机交互（Modares et al. 2015）等领域。

然而，RL仍面临严峻挑战：首先，样本效率低下问题需要大量交互数据支持（Dulac-Arnold et al. 2019）；其次，在物理环境中难以确保安全探索（Thananjeyan et al. 2021）。这些问题在数据采集受限或存在危险性的复杂任务中尤为突出（Pecka and Svoboda 2014）。此外，RL还存在以下局限性：

学习策略在新环境/任务中的泛化能力不足
面临显著的仿真到现实迁移挑战
计算成本高昂且对超参数选择敏感（Dulac-Arnold et al. 2021）
奖励设计可能因引导偏差导致次优策略

值得注意的是，双层优化（BLO）已被引入RL框架：

Stadie等人（2020）将内在奖励建模为BLO问题以实现超参数优化
Hu等人（2024）通过BLO整合强化学习与模仿学习，解决多机器人协同中的耦合行为与信息不全问题
Zhang等人（2020a）提出基于BLO的双层Actor-Critic方法，在协作环境中取得优于纳什均衡的收敛性

然而，这些工作仍局限于传统RL框架，尚未形成系统化的方法论。

元学习的最新进展

元学习近年来受到广泛关注，特别是在深度神经网络训练中的应用(Bengio et al. 1991; Thrun and Pratt 2012)。与传统学习方法不同，元学习通过整合任务集合的数据集和先验知识，能够以极少量数据快速掌握新任务，这种特性在小样本学习场景中尤为显著。目前已发展出多种元学习算法，主要可分为三大类：

基于度量的方法 (Koch et al. 2015; Snell et al. 2017; Chen et al. 2020b; Tang et al. 2020; Gharoun et al. 2023)
基于模型的方法 (Munkhdalai and Yu 2017; Vinyals et al. 2016; Liu et al. 2020b; Co-Reyes et al. 2021)
基于优化的方法 (Finn et al. 2017; Nichol and Schulman 2018; Simon et al. 2020; Singh et al. 2021; Bohdal et al. 2021; Zhang et al. 2024; Choe et al. 2024)

其中，基于优化的方法因其实现简单且性能优越而备受青睐。这类方法通过梯度调整机制，在计算机视觉、自然语言处理等多个领域取得了当前最先进的性能表现。

双层优化(BLO)作为算法框架已广泛应用于基于优化的元学习领域。其中最具代表性的方法当属模型无关元学习(MAML)(Finn et al. 2017)，该方法通过寻找一个初始模型参数，使得基于该参数的梯度下降过程能够快速适应新任务。在后续发展中，研究者们提出了多种MAML改进方案(Grant et al. 2018; Finn et al. 2019, 2018; Jerfel et al. 2018; Mi et al. 2019; Liu et al. 2019; Rothfuss et al. 2019; Foerster et al. 2018; Baik et al. 2020b; Raghu et al. 2019; Bohdal et al. 2021; Zhou et al. 2021; Baik et al. 2020a; Abbas et al. 2022; Kang et al. 2023; Zhang et al. 2024; Choe et al. 2024)。特别值得一提的是，Raghu等(2019)提出的ANIL方法通过仅调整神经网络参数子集实现了高效元学习；Finn等(2019)开发了适用于在线学习的"跟随元领导者"版本；Zhou等(2021)通过挖掘任务间相似性信息提升了MAML的泛化性能；Baik等(2020a)采用自适应学习率和权重衰减系数改进了MAML；Kang等(2023)提出了几何自适应预处理梯度下降方法。

在元正则化研究方面，Denevi等(2018b, 2019, 2018a)、Rajeswaran等(2019)、Balcan等(2019)和Zhou等(2019)提出了一系列改进正则化经验风险最小化偏差的方法。此外，小样本学习领域广泛采用的嵌入框架(Bertinetto et al. 2018; Lee et al. 2019; Ravi and Larochelle 2016; Snell et al. 2017; Zhou et al. 2018; Goldblum et al. 2020; Denevi et al. 2022; Qin et al. 2023; Jia and Zhang 2024)旨在学习跨任务共享的嵌入模型，同时基于嵌入特征为每个任务学习特定参数。

需要特别说明的是，虽然命令式学习(IL)的提出旨在解决上述学习框架在机器人学中的局限性，但其设计具有通用性，可与现有任何学习框架进行集成。例如将强化学习方法构建为IL的上层优化问题，尽管这已超出本文讨论范围。

2.3 神经符号学习

如先前所述，神经符号（NeSy）学习领域尚未形成严格定义的共识，这导致相关文献较为零散且缺乏系统化方法论。本节将简要讨论两大主要研究方向：逻辑推理与物理融合网络，涵盖符号表征既包含离散信号（如逻辑结构）也包含连续信号（如物理属性）的多种应用场景。其他相关研究将在后续章节结合五个机器人自主性案例进行具体分析。

逻辑推理方法

逻辑推理的目标是将可解释且确定性的逻辑规则注入神经网络（Serafini和Garcez 2016；Riegel等2020；Xie等2019；Ignatiev等2018）。部分前人工作通过人类专家直接获取此类知识（Xu等2018；Xie等2019,2021；Manhaeve等2018；Riegel等2020；Yang等2020），或利用可控演绎的预言机（Mao等2018；Wang等2022；Hsu等2023），这类方法被称为演绎法。代表性工作包括DeepProbLog（Manhaeve等2018）、逻辑神经网络（Riegel等2020）和语义损失（Xu等2018）。尽管取得进展，演绎方法仍需要人工提供的结构化形式化符号知识，而这类知识并不总能获取。此外，其扩展性在应对大规模复杂问题时仍显不足。相比之下，归纳方法通过半监督高效网络学习来推导结构化符号表示。一种主流策略基于前向搜索算法（Li等2020b,2022b；Evans和Grefenstette 2018；Sen等2022），但这种方法耗时且难以扩展。其他研究则借助基于梯度的神经网络进行规则归纳，例如SATNet（Wang等2019）、NeuralLP（Yang等2017）和神经逻辑机（NLM）（Dong等2019）。其中，NLM受一阶逻辑启发设计的新型网络架构展现出优于普通神经网络的组合泛化能力。然而，现有归纳算法或仅适用于知识图谱等结构化数据（Yang等2017；Yang和Song 2019），或仅在玩具级图像数据集进行实验（Shindo等2023；Wang等2019）。我们通过IL框架将此类研究推进至机器人领域，为高维图像数据的实际应用提供支持。

物理融合网络

物理融合网络（PINs）通过将物理定律直接整合至神经网络架构与训练过程（Raissi等，2019），旨在增强模型解决复杂科学、工程及机器人学问题的能力（Karniadakis等，2021）。这些网络通过以下方式实现物理规律融合：

损失函数整合：将守恒定律、微分方程等物理原理嵌入损失函数（Duruisseaux等，2023）
约束条件设计：构建物理约束项确保预测符合基本规律
网络结构改进：设计符合物理规律的专用网络模块

该方法显著提升了模型的可解释性、泛化能力和计算效率（Lu等，2021）。典型应用包括：

流体动力学：结合Navier-Stokes方程指导流场预测，即使在数据稀缺区域仍能保持基本流动特性的物理一致性（Sun与Wang，2020）
结构力学：基于变分原理建立应力-应变关系模型，实现高精度结构分析（Rao等，2021）
机器人控制：将刚体动力学方程融入运动规划网络，确保生成轨迹满足物理可行性（Han等，2024）

物理融合网络（PINs）已成功应用于机器人自主性的多个关键任务：

环境感知：通过物理约束提升感知精度（Guan等，2024）
运动规划：将机器人运动学模型嵌入规划网络（Romero等，2023）
精准控制：融合动力学模型实现高精度控制（Han等，2024）

通过将机器人系统的运动学与动力学直接嵌入学习过程，PINs使机器人能够：

更精确地预测物理交互结果
实时生成符合物理规律的响应策略
显著提升操作安全性与任务执行效率

主要实现方法有

物理定律网络嵌入
将牛顿定律、拉格朗日方程等基础物理原理编码至网络结构（Zhao等，2024）
初始/边界条件约束
在训练过程中强制施加物理系统的初始条件与边界约束（Rao等，2021）
能量函数优化
通过最小化表征物理系统特性的能量泛函构建损失函数（Guan等，2024）

3 命令式学习

3.1 体系结构

如图1所示的命令式学习(IL)框架包含三个核心模块：神经系统、推理引擎和记忆模块。具体而言，神经系统负责从原始传感器数据（如图像、激光雷达点云、惯性测量单元数据及其组合）中提取高层次语义属性。这些语义属性随后被传输至推理引擎——这是一个基于物理原理、逻辑推理、解析几何等符号化过程实现的计算模块。记忆模块则负责存储机器人的运行经验和习得知识，包括环境数据、符号规则和物理世界地图等信息，支持长期或短期记忆存储。此外，推理引擎会与记忆模块进行一致性校验，据此更新记忆内容或实施必要的自我修正。

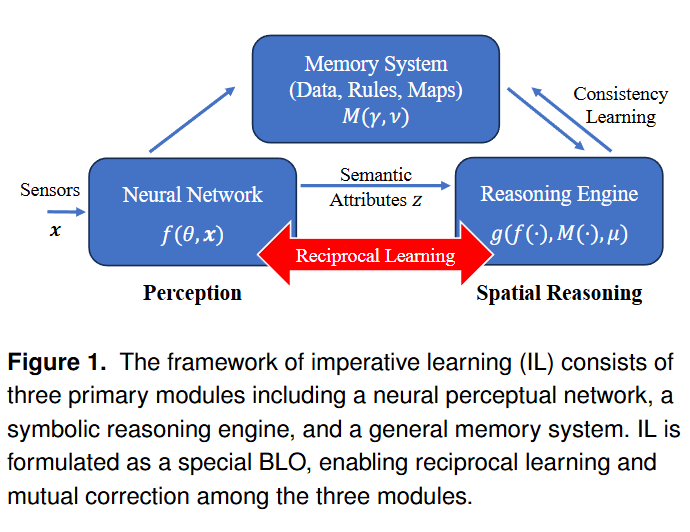
命令式学习(IL)框架由三个核心模块构成：神经感知网络、符号推理引擎和通用记忆系统。该框架被建模为一种特殊的双层优化(BLO)问题，能够实现三个模块间的协同学习与相互校正机制。

该架构设计通过整合神经系统的特征表达能力、推理引擎的可解释性与泛化能力，以及记忆模块的信息保持特性，构建起统一的智能框架。下文将阐述实现这一设计目标的数学原理。

3.2 形式化建模

框架的最重要特性在于，神经模块、推理模块和记忆模块能够通过自监督方式实现协同学习。这一特性通过将框架建模为双层优化问题（Bilevel Optimization, BLO）实现。

我们将神经系统定义为 $\bm z = f({\bm{\theta}}, \bm{x})$ ，其中 $\bm{x}$ 表示传感器测量值， ${\bm{\theta}}$ 表示感知相关可学习参数， $\bm z$ 表示语义属性等神经输出；推理引擎定义为 $g(f, M, {\bm{\mu}})$ ，其中 ${\bm{\mu}}$ 为推理相关参数；记忆系统定义为 $M({\bm{\gamma}}, {\bm{\nu}})$ ，其中 ${\bm{\gamma}}$ 为感知相关记忆参数， ${\bm{\nu}}$ 为推理相关记忆参数。基于此，我们的命令式学习（Imperative Learning, IL）可形式化为特殊形式的双层优化问题：

$\min_{ \bm \psi \doteq [{\bm{\theta}}^\top,~{\bm{\gamma}}^\top]^\top} U\left(f({\bm{\theta}}, \bm{x}), g({\bm{\mu}}^*), M({\bm{\gamma}}, {\bm{\nu}}^*)\right)$

$\textrm{s.t.} \quad \bm \phi^* \in \arg\min_{ \bm \phi \doteq [{\bm{\mu}}^\top,~{\bm{\nu}}^\top]^\top} L(f({\bm{\theta}}, \bm{x}), g({\bm{\mu}}), M({\bm{\gamma}}, {\bm{\nu}}))$

$\textrm{s.t.} \quad \xi(M({\bm{\gamma}}, {\bm{\nu}}), {\bm{\mu}}, f({\bm{\theta}}, \bm{x})) = \text{ or } \leq 0$

其中： $\xi$ 表示通用约束（等式或不等式）； $U$ 和 $L$ 分别为上层（Upper-Level, UL）和下层（Lower-Level, LL）损失函数； $\bm \psi \doteq [{\bm{\theta}}^\top, {\bm{\gamma}}^\top]^\top$ 为上层变量组合， $\bm \phi \doteq [{\bm{\mu}}^\top, {\bm{\nu}}^\top]^\top$ 为下层变量组合。在特定应用场景中， $U$ 和 $L$ 也可分别称为神经损失和符号损失。

"命令式"这一术语用于强调学习过程的被动特性：经优化后，上层损失中的神经系统 $f$ 将在约束 $\xi$ 的引导下，与下层推理引擎 $g$ （如逻辑推理、物理规律或几何分析过程）保持对齐，从而生成符合逻辑、物理定律或几何约束的语义属性或谓词。在某些应用中， $\bm \psi$ 和 $\bm \phi$ 也可称为类神经元参数和类符号参数。

自监督学习机制

如简介所述，命令式学习（IL）的建模灵感源于一个重要发现：包括几何推理、物理推理和逻辑推理在内的多种符号推理引擎，均可在无监督条件下完成优化。典型例证包括：

逻辑推理：如方程发现（Billard等, 2002）与A*搜索算法（Hart等, 1968）
几何推理：捆集调整（Bundle Adjustment, BA）（Agarwal等, 2010）
物理推理：模型预测控制（Kouvaritakis等, 2016）

IL框架通过双层优化（BLO）联合优化神经模块、推理引擎与记忆系统，构建三者的互校正机制。这种设计使得所有模块仅通过环境观察即可实现自监督的协同进化。其核心优势体现在：

无标签依赖：利用符号推理引擎的自我优化能力
动态适应性：通过实时交互持续更新知识表征
错误校正：模块间的双向反馈避免误差累积

值得注意的是，尽管IL专为自监督学习设计，但通过在上层（UL）或下层（LL）损失函数（或同时）引入标注数据，可灵活扩展至监督学习或弱监督学习场景。这种兼容性使IL能适应从完全无监督到半监督的多样化训练需求。

记忆系统

命令式学习(IL)框架中的记忆系统是一个具备在线信息存储与检索能力的通用组件。具体而言：

基本定义
可以是任何支持数据写入和读取操作的结构（Wang等, 2021）
实现形式
1. 神经网络形式
  通过参数存储信息（如神经辐射场[NeRF]模型，Mildenhall等, 2021），利用数学运算或隐式映射进行信息读取
2. 显式物理表征
  - 在线构建的环境地图
  - 在线推导的逻辑规则集合
  - 实时采集的原始数据集
3. 大语言模型记忆系统
  采用文本形式的检索增强生成（RAG, Lewis等, 2020）技术，实现符号知识的写入、读取与管理

该设计赋予记忆系统多模态信息处理能力，支持从原始传感器数据到抽象符号知识的多层次表征存储。通过双层优化机制，记忆内容可随环境交互动态更新，确保知识体系的持续进化。

3.3 优化方法

双层优化（BLO）已在元学习（Finn等，2017）、超参数优化（Franceschi等，2018）和强化学习（Hong等，2020）等框架中得到探索。然而，大多数理论分析主要集中于它们在数据驱动模型中的适用性，其中一阶梯度下降（GD）常被采用（Ji等，2021；Gould等，2021）。尽管如此，许多推理任务存在独特的挑战，使得GD效果受限。例如：

几何推理（如捆集调整[BA]）需要二阶优化器（Fu等，2024），例如Levenberg-Marquardt（LM）算法（Marquardt，1963）
多机器人路径规划需要对离散变量进行组合优化（Ren等，2023a）

在BLO框架中应用此类LL优化会引入极端复杂性挑战，相关研究仍处于探索阶段（Ji等，2021）。因此，我们将首先深入探讨通用BLO，然后在我们的IL框架中提供涵盖LL优化不同挑战的实际示例。

求解 IL 方程的主要任务是计算 UL 参数 ${\bm{\theta}}$ 和 ${\bm{\gamma}}$ 以及 LL 参数 ${\bm{\mu}}$ 和 ${\bm{\nu}}$ 。

直观上，UL 参数通常类似于神经网络中的权重，可以通过 UL 目标函数 $U$ 的梯度进行更新：

$\begin{aligned} \nabla_{\bm{\theta}} U &= \frac{\partial U}{\partial f} \frac{\partial f}{\partial {\bm{\theta}}} + \frac{\partial U}{\partial g} \frac{\partial g}{\partial {\bm{\mu}}^*} \color{blue}{\frac{\partial {\bm{\mu}}^*}{\partial {\bm{\theta}}}} + \frac{\partial U}{\partial M} \frac{\partial M}{\partial {\bm{\nu}}^*} \color{blue}{\frac{\partial {\bm{\nu}}^*}{\partial {\bm{\theta}}}}, \\ \nabla_{\bm{\gamma}} U &= \frac{\partial U}{\partial M} \frac{\partial M}{\partial {\bm{\gamma}}} + \frac{\partial U}{\partial g} \frac{\partial g}{\partial {\bm{\mu}}^*} \color{blue}{\frac{\partial {\bm{\mu}}^*}{\partial {\bm{\gamma}}}} + \frac{\partial U}{\partial M} \frac{\partial M}{\partial {\bm{\nu}}^*} \color{blue}{\frac{\partial {\bm{\nu}}^*}{\partial {\bm{\gamma}}}}. \end{aligned}$

计算上述公式中的关键挑战在于蓝色部分的隐式求导，其形式如下：

$\color{blue}{ \frac{\partial \bm \phi^*}{\partial \bm \psi} = \begin{bmatrix} \frac{\partial \bm \mu^*}{\partial \bm \theta} & \frac{\partial \bm \mu^*}{\partial \bm \gamma} \\ \frac{\partial \bm \nu^*}{\partial \bm \theta} & \frac{\partial \bm \nu^*}{\partial \bm \gamma} \end{bmatrix} }$

其中 ${\bm{\mu}}^*$ 和 ${\bm{\nu}}^*$ 是 LL 问题的解。

为了简化表示，可以将上述公式写成矩阵形式：

$\nabla_{\bm{\psi}} U = \frac{\partial U}{\partial \bm \psi} + \frac{\partial U}{\partial \bm \phi^*} \color{blue}{\frac{\partial \bm \phi^*}{\partial {\bm{\psi}}}},$

其中：

$\frac{\partial U}{\partial \bm \psi} = \left[\left(\frac{\partial U}{\partial f} \frac{\partial f}{\partial {\bm{\theta}}}\right)^\top,\left(\frac{\partial U}{\partial M} \frac{\partial M}{\partial {\bm{\gamma}}}\right)^\top\right]^\top$ ，
$\frac{\partial U}{\partial \bm \phi^*} = \left[\left(\frac{\partial U}{\partial g} \frac{\partial g}{\partial {\bm{\mu}}^*}\right)^\top, \left(\frac{\partial U}{\partial M} \frac{\partial M}{\partial {\bm{\nu}}^*}\right)^\top \right]^\top$ 。

通常有两种方法来计算这些梯度：展开（unrolled）求导 和 隐式求导（implicit differentiation）。我们在下面的算法中总结了一个结合两者的通用框架，以帮助更清晰地理解整体流程。

展开求导（Unrolled Differentiation）

展开求导是一种易于实现的双层优化（BLO）问题求解方法。它依赖于对下层优化过程进行自动微分（AutoDiff）。具体而言，给定下层变量的初始值 $\bm \phi_0 = \bm \Phi_0(\bm \psi)$ ，在第 $t=0$ 步，展开优化的迭代过程为：

$\bm \phi_t = \bm \Phi_t( \bm \phi_{t-1}; \bm \psi), \quad t = 1, \cdots, T,$

其中， $\bm \Phi_t$ 表示基于特定下层问题的更新方式， $T$ 是迭代步数。

一种常见的更新方式是基于梯度下降：

$\bm \Phi_t (\bm \phi_{t-1}; \bm \psi) = \bm \phi_{t-1} - \eta \cdot \frac{\partial {L} (\bm \phi_{t-1}; \bm \psi)}{\partial \bm \phi_{t-1}},$

其中， $\eta$ 是学习率，梯度项 $\frac{\partial {L} (\bm \phi_{t-1}; \bm \psi)}{\partial \bm \phi_{t-1}}$ 可以通过自动微分获得。

因此，我们可以用 $\bm \phi_T = [\bm \mu_T, \bm \nu_T]$ 近似代替最优解 $\bm \phi^* = [\bm \mu^*, \bm \nu^*]$ ，从而计算出 $\nabla_{\bm{\theta}} {U} (\bm{\theta})$ 和 $\nabla_{\bm{\gamma}} {U} (\bm{\gamma})$ 。

完整的展开系统定义为：

$\bm \Phi(\bm \psi) = (\bm \Phi_T \circ \cdots \circ \bm \Phi_1 \circ \bm \Phi_0)(\bm \psi),$

其中 $\circ$ 表示函数复合。

因此，我们只需优化如下替代问题：

$\min_{\bm{\psi}} \;\; U(\bm \psi, \bm \Phi(\bm \psi)),$

在这个形式中， $\frac{\partial \bm \Phi(\bm \psi)}{\partial \bm \psi}$ 可以通过自动微分求得，而无需显式计算公式 \eqref{implicit_part} 中的四个偏导项。

隐式求导（Implicit Differentiation）

隐式求导方法直接计算导数 $\color{blue} \frac{\partial \bm \phi^*}{\partial \bm \psi}$ 。

我们介绍一种通用的隐式求导算法框架，它通过求解下层问题一阶最优性条件所构成的线性系统获得隐式导数。具体的解法依赖于任务，将在应用部分中通过示例说明。

假设 $\bm \phi_T = [\bm \mu_T, \bm \nu_T]$ 是用通用优化器在 $T$ 步中得到的下层问题~\eqref{eq:low-il}的解（可能带有约束~\eqref{eq:il-constraint}），则上层梯度的近似为：

$\hat \nabla_{\bm{\psi}} U \approx \frac{\partial U}{\partial \bm \psi} \Big|_{\bm\phi_T} + \frac{\partial U}{\partial \bm \phi^*}{\color{blue}\frac{\partial \bm\phi^*}{\partial {\bm{\psi}}}}\Big|_{\bm \phi_T}.$

接下来，通过下层问题的最优性条件 $\frac{\partial \tilde L}{\partial \bm \phi^*} = \bm 0$ 构建隐式方程，并对其两边关于 $\bm \psi$ 求导，有：

$\frac{\partial^2 \tilde{L} (\bm \phi^*(\bm\psi), \bm \psi)}{\partial \bm \phi^*(\bm\psi)\partial \bm \psi} + \frac{\partial^2 \tilde{L} (\bm \phi^*(\bm\psi), \bm \psi)}{\partial \bm \phi^*(\bm\psi)\partial \bm \phi^*(\bm \psi)} \cdot {\color{blue} \frac{\partial \bm \phi^* (\bm \psi)}{\partial \bm \psi}} = \bm 0.$

求解上式得到隐式梯度为：

${\color{blue} \frac{\partial \bm \phi^* (\bm \psi)}{\partial \bm \psi}} = - \underbrace{ \left( \frac{\partial^2 \tilde{L}}{\partial \bm \phi^* \partial \bm \phi^*} \right)^{-1} }_{\bm H_{\bm \phi^* \bm \phi^*}^{-1}} \underbrace{ \frac{\partial^2 \tilde{L}}{\partial \bm \phi^* \partial \bm \psi}}_{\bm H_{\bm \phi^* \bm \psi}}.$

这表示我们通过 Hessian 矩阵的求逆得到了隐式梯度。

⚠️ 注意：在实践中，Hessian 矩阵可能太大而无法直接计算或存储[^2]，因此我们可以通过解线性系统来规避它。

代入该隐式梯度后，上层梯度为：

$\begin{aligned} \nabla_{\bm\psi} {U} &= \frac{\partial {U}}{\partial \bm\psi} - \underbrace{\frac{\partial {U}(\bm{\psi}, \bm{\phi}^*)}{\partial \bm \phi^*} }_{\bm v^\top} \bm H_{\bm \phi^* \bm \phi^*}^{-1} \cdot \bm H_{\bm \phi^* \bm \psi} \\ &= \frac{\partial {U}}{\partial \bm\psi} - \bm q^\top \cdot \bm H_{\bm \phi^* \bm \psi}. \end{aligned}$

我们可以通过以下优化问题来求解线性系统 $\bm H \bm q = \bm v$ ：

$\bm q^* = \arg\min_{\bm q} Q (\bm q) = \arg\min_{\bm q} \left(\frac{1}{2} \bm q^\top \bm H \bm q - \bm q^\top \bm v \right),$

其中 $\bm H = \bm H_{\bm \phi^* \bm \phi^*}$ 简写。

该线性系统可通过共轭梯度法或梯度下降等方法求解，无需显式存储或反转 Hessian。更新公式如下：

$\bm q_{k} = \bm q_{k-1} - \eta \left(\bm H \bm q_{k-1} - \bm v\right).$

该算法高效的原因是我们可使用 Hessian-向量乘的技巧，即：

$\bm H \bm q = \frac{\partial^2 \tilde{L}}{\partial \bm \phi \partial \bm \phi } \cdot \bm q = \frac{\partial \left(\frac{\partial \tilde{L}}{\partial \bm \phi} \cdot \bm q \right)}{\partial \bm \phi},$

其中 $\frac{\partial \tilde{L}}{\partial \bm \phi}\cdot \bm q$ 是一个标量。这意味着不需要显式构造 Hessian。

我们在算法中总结了隐式求导流程。请注意，最优性条件依赖于具体的下层问题：

对于无约束问题， $\tilde{L}$ 即为损失函数本身；
对于带约束问题， $\tilde{L}$ 是拉格朗日函数。

[^2]: 举例来说，若上层和下层模型都有一个仅有 100 万个参数的神经网络（使用 32-bit float），则存储每个网络只需约 4MB。但对应的 Hessian 矩阵大小为 $10^6 \times 10^6 \times 4$ 字节，即 4TB，远远超过一般设备的内存容量。

近似方法（Approximation）

隐式求导虽然强大，但实现起来较为复杂。为此，一种常见的近似方法是忽略隐式部分，仅使用直接部分：

$\hat \nabla_{\bm{\psi}} U \approx \frac{\partial U}{\partial \bm \psi}\Big|_{\bm{\phi}_T}$

这等价于在上层优化中将下层解 ${\bm{\phi}}_T$ 视为常数。

该近似方式计算更高效，但会引入误差项：

$\epsilon \sim \left| \frac{\partial U}{\partial \bm \phi^*}\frac{\partial \bm\phi^*}{\partial {\bm{\psi}}} \right|.$

尽管存在误差，在某些场景中仍然非常有用，特别是当隐式导数包含了很小的二阶导数乘积时（这通常依赖于具体的下层问题）。

值得一提的是，在 IL 框架中：

感知相关的参数 $\bm \psi$ 被分配到上层神经网络损失（UL）中；
推理相关的参数 $\bm \phi$ 被分配到下层符号损失函数（LL）中。

这种设计有两个关键考虑：

避免计算大型 Jacobian 和 Hessian 矩阵

神经网络中包含的类神经变量（如 $\bm \phi$ ）常常有上百万参数。例如，矩阵 $\bm H_{\bm \phi^* \bm \phi^*}$ 非常庞大，如果将其用于 LL 优化的隐式导数计算，计算成本极高。将这些变量放在上层损失中能有效规避这个问题。
不同类型的优化器适应性不同

感知相关参数通常使用 SGD 等一阶优化器（如 \citep{sutskever2013importance}），但这些方法对几何类符号问题并不适用，后者更依赖二阶优化器（如 \citep{wang2023pypose} 所示）。因此，将感知参数与推理参数分离，使得 IL 中的双层优化问题（BLO）更易分析和求解。

总之，这种分离策略虽然不是强制的，但在多数实际下层任务中是有益的。